二分查找 | 江南笑书生

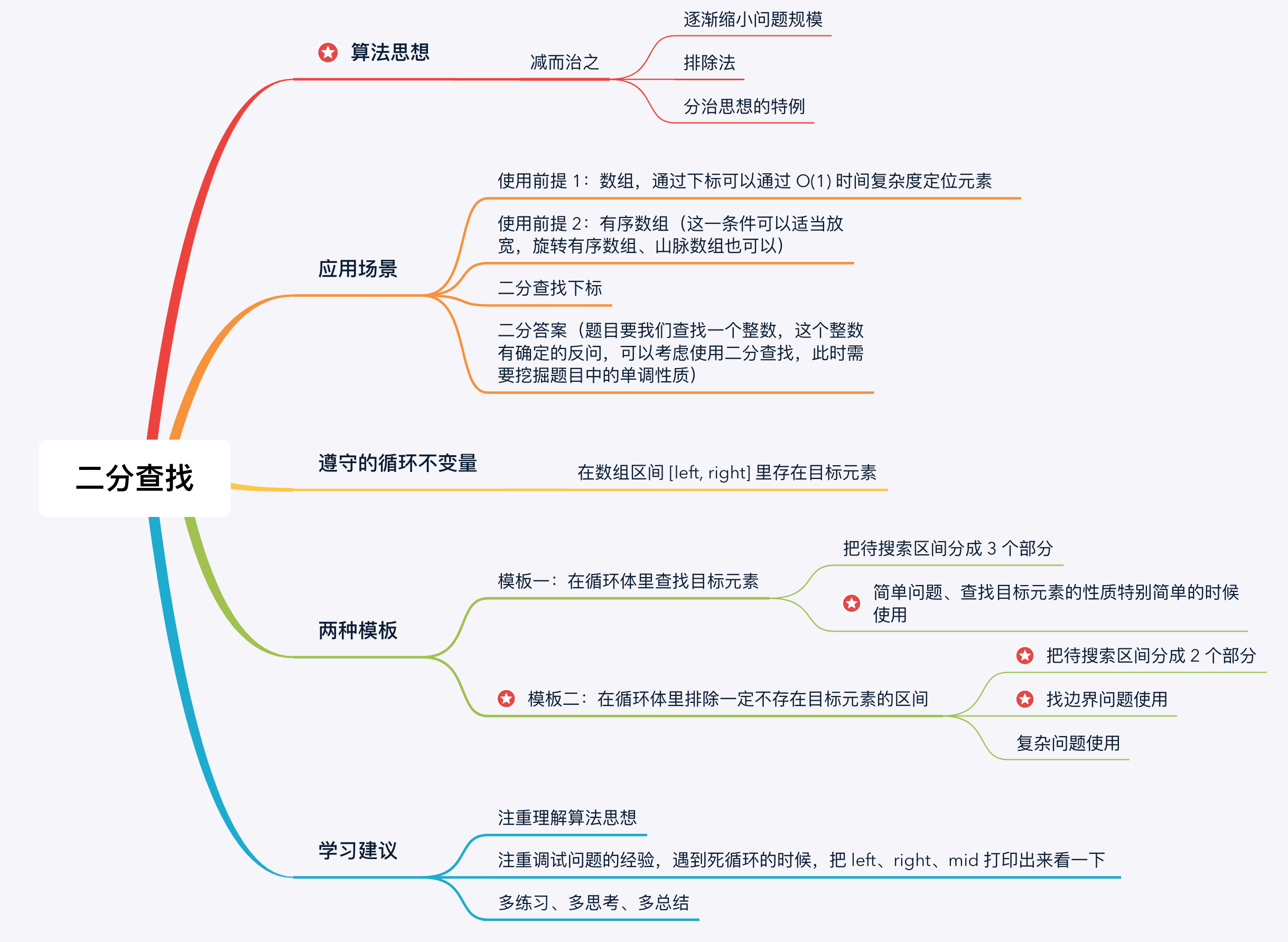
注：图源 liweiwei1419

二分查找使用前提：有序表顺序存储，通常是有序数组。

二分查找算法思想

在有序顺序表中，取中间元素与目标元素比较：

若相等，即找到目标元素，算法结束；
若小于目标元素，则在右半区间继续进行二分查找；
若大于目标元素，则在左半区间继续进行二分查找。

重复上述过程，直至找到目标元素，或所有查找区间无目标元素，算法结束。

二分查找基础问题

704. 二分查找

在此问题中，二分查找将待查找数组分为了 3 个部分：mid，mid 左边，mid 右边。

若 mid 就是待查找元素，直接返回即可；否则根据不等条件，去左半区间或右半区间查找即可。

二分查找每次都将查找范围减半，因此大大降低了算法的时间复杂度，达到了 O(logn)。

下面是 704. 二分查找的参考代码：

class Solution {
    /**
     * 二分查找
     * 时间复杂度：O(logn)
     * 空间复杂度：O(1)
     * 
     * @param nums
     * @param target
     * @return
     */
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

此题是最基础的二分查找，代码可作为二分查找的模板使用。

二分查找代码中最需要注意的地方是 while 循环条件 和 mid 取值 的设置。

mid 赋值语句通常会写成：

1	int mid = (left + right) / 2;

不过这种写法存在隐患。当 left 和 right 都很大时，left + right 可能会发生整型溢出。因此最好写成如下形式：

1	int mid = left + (right - left) / 2;

这两种写法其实没有太大区别，因为绝大多数问题中，数组下标都不会取到特别大。

另外，还可以参考 JDK 源码 java.util.Arrays 二分查找方法中的写法：

while (low <= high) {
    int mid = (low + high) >>> 1;
    long midVal = a[mid];

    if (midVal < key)
        low = mid + 1;
    else if (midVal > key)
        high = mid - 1;
    else
        return mid; // key found
}

注：>>> 按位右移补零操作符。左操作数的值按右操作数指定的位数右移，移动得到的空位以零填充。

int mid = (low + high) >>> 1 在 low + high 发生整型溢出时，高位补0，结果依然正确。

为什么是 1/2

为什么是二分查找，而不是三分、四分？

例如：在取值范围 0~1000000 之间 1000 个元素从小到大均匀分布的数组中查找 5。

从较小数组下标开始查找显然要比从数组中间开始查找更为快捷。
$$
mid = left + \frac{1}{2} \left ( right - left \right )
$$
将上式中的 $1/2$ 进行改进，改进为下面的计算方案：
$$
mid = left + \frac{target - nums[left]}{nums[right] - nums[left]} \left ( right - left \right )
$$
这样改进有什么好处呢？

假设 nums = {0, 1, 16, 24, 35, 47, 59, 62, 73, 88, 99} ，left = 1，right = 10，则 nums[left] = 1, nums[right] = 99。如果目标值 target = 16，二分查找需要 4 次，而采用新的方案：
$$
mid = 1 + \frac{16 - 1}{99 - 1} \left ( 10 - 1 \right ) = 2.378
$$
取整 mid = 2，只需要 2 次即可找到目标值。

其实，这就是另一种有序顺序表的查找算法：插值查找。

插值查找（Interpolation Search），根据要查找的目标元素 target 与查找表中 nums[left]、nums[right] 比较后的查找算法，其核心就在于插值的计算公式 $\frac{target - nums[left]}{nums[right] - nums[left]}$ 。

从时间复杂度来讲，插值查找也是 O(logn)。对于表长较大，而元素分布又比较均匀的查找表来说，插值查找的平均性能要优于二分查找。不过在我们对问题一无所知的时候，取中间数是最好的做法。

参考：

用减治思想写二分查找问题、几种模板写法的介绍与比较
《大话数据结构》8.4 有序表查找